Determining a central mass from observations of its satellites

This is based on an experiment Ben and I did in our first year at Keele. Its was a good experiment that produced some surprisingly accurate results.

Kepler's Third Law states

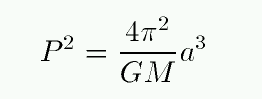
The plan of the experiment is to fill in each of the variables(Period P and Radius a).

First things first is you need to acquire images of the thing you wish to determine the mass of, about 10 spaced over an adequate timescale (would depend on system observed). In the case of the experiment Ben and I conducted we had 7 images of Uranus over a period of 240 days.

Next Use a program that allows you to "blink" between images (we used SAOImage) and Find the bodies which are moving in the images. This can be quite difficult as the central body is most likely moving also relative to the background, this is why it is good to have a couple of images closer together. As there will be only a small change in the background-the moon should change position in a much smaller period. Once the satellites have been identified mark their positions on each image.

Then using the imaging program find the (central) x,y co-ordinates for each body and the central mass in each image. The relative positions of the satellites from the central body. Using these values its just a case of using the Pythagorean theorem (a^2 + b^2 = c^2) to calculate the radius of the orbit in pixels. Convert the radius into Kilometers.

Going back to the relative positions and using an ATAN2 function to convert the x,y co-ordinates into a relative angle to the central mass. Then using n Pi (where n is an integer value) to adjust so an angle against time is a straight line graph - this is needed due to definition of the ATAN2 function . The gradient of such a graph is the angular frequency ω of orbit. From the angular frequency ω we can find the period P of the orbit using the relation below.

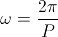
Once the period is known it is just a case of rearranging Kepler's third law for Mass M and you have the mass of the central body